Solving the following problem helped me better understand how to traverse a matrix and how to get the valid neighbors of a cell in the matrix

Problem statement

An image is represented by an m x n integer grid image where image[i][j] represents the pixel value of the image.

You are also given three integers sr, sc, and newColor. You should perform a flood fill on the image starting from the pixel image[sr][sc].

To perform a flood fill, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color), and so on. Replace the color of all of the aforementioned pixels with newColor.

Return the modified image after performing the flood fill.

Understand

Input: image = [[1,0,1,1],[1,1,1,1]] , sr=1, sc=1, newColor=2

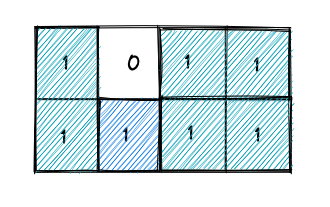
Output: [[2,0,2,2],[2,2,2,2]]

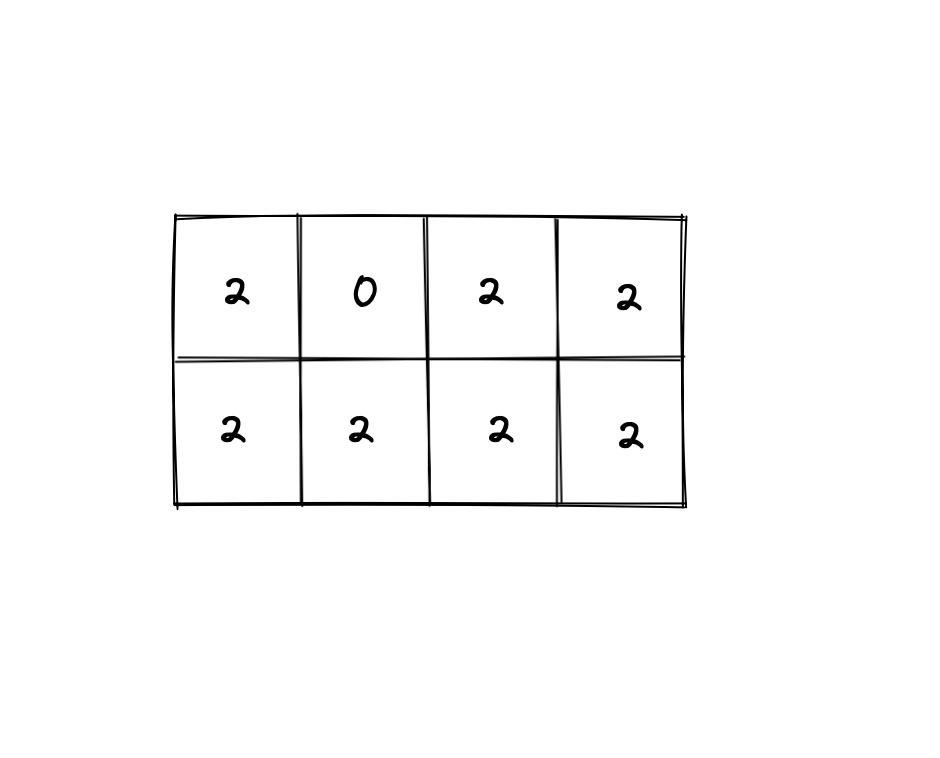
Explanation:
- we have to perform flood fill from the cell with row = sr and column = sc
- in this example we can perform flood fill on the cells left, right and above the cell (sr,sc) and change their values to newColor only if image[row][col] == image[sr][sc]
- since the image[sr-1][sc] != image[sr][sc], we do not change it’s value
- change the values of the neighbors of the cells you visit

Input: image = [1,1,1]], sr=0, sc=1, newColor=2
Output: [[2,2,2]]

Input: image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, newColor = 2
Output: [[2,2,2],[2,2,0],[2,0,1]]

Input: image = [[0,0,0],[0,0,0]], sr = 0, sc = 0, newColor = 2
Output: [[2,2,2],[2,2,2]]

Match

Techniques

since it’s already given that we have to consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, we can perform either DFS or BFS from image[sr][sc] and reach it’s valid neighbor to change the value to newColor
in this post we will look at both bfs and dfs implementation
we change the value only if the value of the is equal to image[sr][sc] value

Plan

def function(image, sr, sc, newColor):
    source = image[sr][sc]
    image[sr][sc] = newColor
    call dfs on image[sr][sc]
    return image

def dfs():
    dfs from sr,sc
    get valid neighbors for (sr,sc)
        if image[row][col] == source:
            image[row][col] = newColor

def bfs():

Implement

class Flood_fill:
    def valid_neighbors(self, r,c,image):
        valid = []
        neighbors = [(r+1,c),(r-1,c),(r,c+1),(r,c-1)]
        for (nr,nc) in neighbors:
            if len(image) > nr >= 0 and len(image[0]) > nc >= 0:
                valid.append((nr,nc))
        return valid
        
    def dfs(self, row, col, source, image, color, visited):
        for (nr,nc) in self.valid_neighbors(row, col, image):
            if (nr,nc) not in visited:
                visited.add((nr,nc))
                if image[nr][nc] == source:
                    image[nr][nc] = color
                    self.dfs(nr,nc,source,image, color, visited)
    
    def bfs(self, row, col, image, visited, source, color):
        queue = [(row, col)] 
        while queue:
            r, c = queue.pop(0)
            for (nr,nc) in self.valid_neighbors(r, c, image):
                if (nr,nc) not in visited:
                    if image[nr][nc] == source:
                        image[nr][nc] = color
                        queue.append((nr,nc))
                        visited.add((nr,nc))

    def floodFill(self, image: List[List[int]], sr: int, sc: int, newColor: int) -> List[List[int]]:
        source = image[sr][sc]
        image[sr][sc] = newColor
        for row in range(len(image)):
            for col in range(len(image[0])):
                if row==sr and col==sc:
                    self.dfs(row, col, source, image, newColor, set())
                    # to call bfs 
                    visited = set()
                    self.bfs(row, col, image, visited, source, newColor)
                    visited.add((row,col))
        return image

Review

consider the input: image = [[1,1,1],[1,1,0],[1,0,1]], sr = 1, sc = 1, newColor = 2
the bfs traversal of the matrix is shown in the figure below
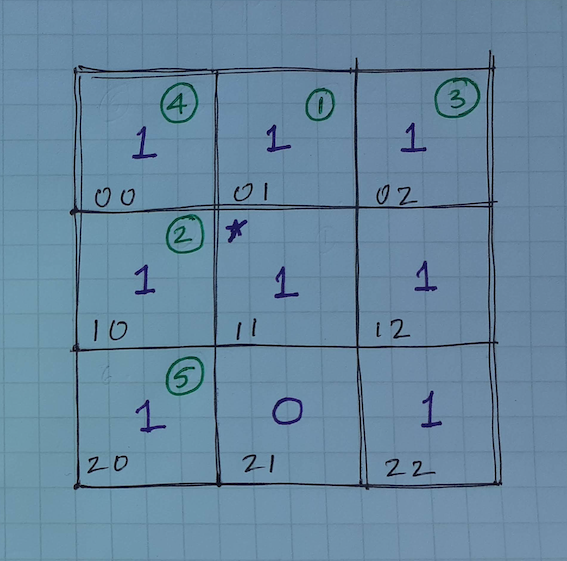
- the numbers in green and that are circled represent the order in which the cells are visited
status of the queue while doing a bfs traversal
1 1 [(2, 1), (0, 1), (1, 2), (1, 0)]
0 1 [(1, 1), (0, 2), (0, 0)]
1 0 [(2, 0), (0, 0), (1, 1)]
0 2 [(1, 2), (0, 1)]
0 0 [(1, 0), (0, 1)]
2 0 [(1, 0), (2, 1)]
the dfs traversal of the matrix is shown in the figure below
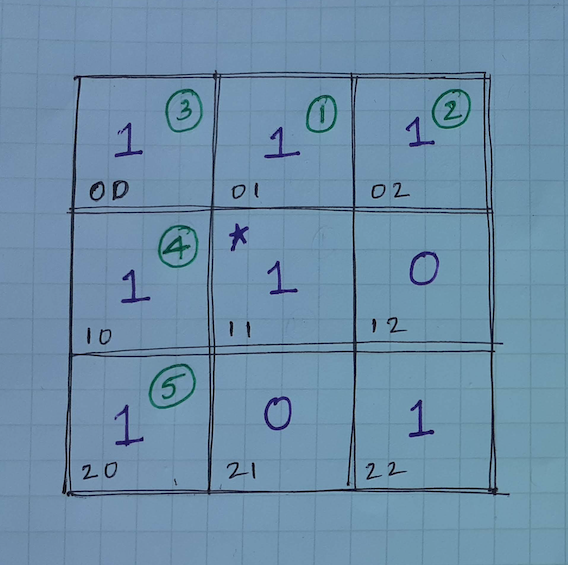
- the numbers in green and that are circled represent the order in which the cells are visited
status of the stack while doing a dfs traversal
1 1 [(2, 1), (0, 1), (1, 2), (1, 0)]
0 1 [(2, 1), (0, 1), (1, 2), (1, 0)]
0 2 [(1, 1), (0, 2), (0, 0)]
0 0 [(1, 1), (0, 2), (0, 0)]
1 0 [(1, 0), (0, 1)]
2 0 [(2, 0), (0, 0), (1, 1)]

Evaluate

complexity:
- time: O(n) where n=number of pixels in the image
- space: O(n) size of call stack while calling dfs