Kth largest value of binary search tree
The following problem helped me understand that in-order traversal of a binary search tree yields a sorted array.

Problem statement
Write a function that takes in a Binary Search Tree(BST) and a positive integer k and returns the kth largest integer contained in the BST
Assume the following:
- there will only be integer values in the BST
- k <= number of nodes in the BST
- if tree = [5, 7, 7] second largest value of the BST will be 7 and not 5
Understand
Input: [15, 5, 20, 2, 5, 17, 22, 1, 3],k = 3
Output: 17
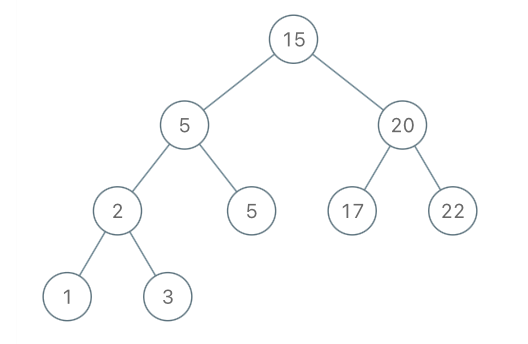
Explanation: after 22 and 20, 17 is the largest values in the given BST
Input: [1], k=1
Output: 1
Input: [1], k=2
Output: not a valid case
Input: [2,1,3], k=3
Output: 3
Input: [1,null,2,null,3,null,4], k=0
Output: Not a valid case
Match
List
// traverse tree
build node_list
// sort nodes_list in descending order
// return node_list[k]
- complexity:
- time: O(n)+O(n log n) -> O(n log n)
- space: O(n)
Linked list
- using linked list will cost us extra time to create a liked list
Hashmap asd Hashset
- both the data structure are not useful for solving the problem
Stack and Queue
- we are not required to look for or maintain LIFO or FIFO order
Heap
- Heap are very helpful to find the kth largest or kth smallest elements
// create max heap // pop k times // return kth popped item - complexity:
- time: O(n) + O(n log n) -> O(n log n)
- space: O(n)
- all though with heap we can obtain the kth element, it did not improve the complexity of the algorithm that we came up by using list
Techniques
- we can traverse a tree using BFS or DFS
- DFS has preorder, postorder and inorder traversal
Exploring the traversals
- let us consider out first example, tree = [15,5,20,2,5,17,22,1,3] and check the order of the nodes that we visit with each traversal
Breadth first search
- bfs traversal of BST = [[1],[2,3],[5,5,15,17],[20,22]]
Preorder traversal
- preorder traversal of BST = [15,5,20,2,5,17,22,1,3] is [15,5,2,1,3,5,20,17,22]
Postorder traversal
- postorder traversal of BST = [15,5,20,2,5,17,22,1,3] is [1,3,2,5,5,17,22,20,15]
Inorder traversal
-
inorder traversal of BST = [15,5,20,2,5,17,22,1,3] is [1,2,3,5,5,15,17,20,22]
- comparing all the traversals it is safe to conclude that in-order traversal yields a sorted array
- taking advantage of this property we can arrive at the solution arrive at the solution
- high level steps involved are
- traverse tree in inorder fashion - build array of nodes
- return array[len(array)-k]
// dfs - inorder recursive
// list of nodes
// return kth element from end
- complexity:
- time: O(n)
- space: O(n)+O(n) -> O(n)
- we could traverse the tree in reverse in-order to get the list of values in descending order
- we can do so by adding left child on to the stack an then the right child so the right child is processed before the left child
// reverse in-order -> recursion
// list of nodes
// return kth element
- complexity:
- time: O(n)
- space: O(n)+O(n)
Implementation
class BST:
def __init__(self, value, left=None, right=None):
self.value = value
self.left = left
self.right = right
def reverse_inorder(root, array, k):
if root == None:
return None
node = root
stack = [node]
while stack:
if node == None:
node = stack.pop()
array.append(node.value)
node = node.left
else:
stack.append(node)
node = node.right
def findKthLargestValueInBst(tree, k):
if tree == None:
return None
nodes_list = []
reverse_inorder(tree, nodes_list, k)
return nodes_list[k-1]
Review
- for the input tree [15, 5, 20, 2, 5, 17, 22, 1, 3] and k = 3
- nodes_list = [22, 20, 17, 15, 5, 5, 3, 2, 1, 15]
Evaluate:
- complexity:
- traverse tree -> time: O(n)
- nodes_list + call stack -> space: O(n)+O(n)