Binary tree to a linked list
I found this problem interesting because it combines the concept of linked list and binary tree traversal.

Problem statement
Given the root of a binary tree, flatten the tree into a “linked list”:
-
The “linked list” should use the same TreeNode class where the right child pointer points to the next node in the list and the left child pointer is always null.
-
The “linked list” should be in the same order as a pre-order traversal of the binary tree.
Understand
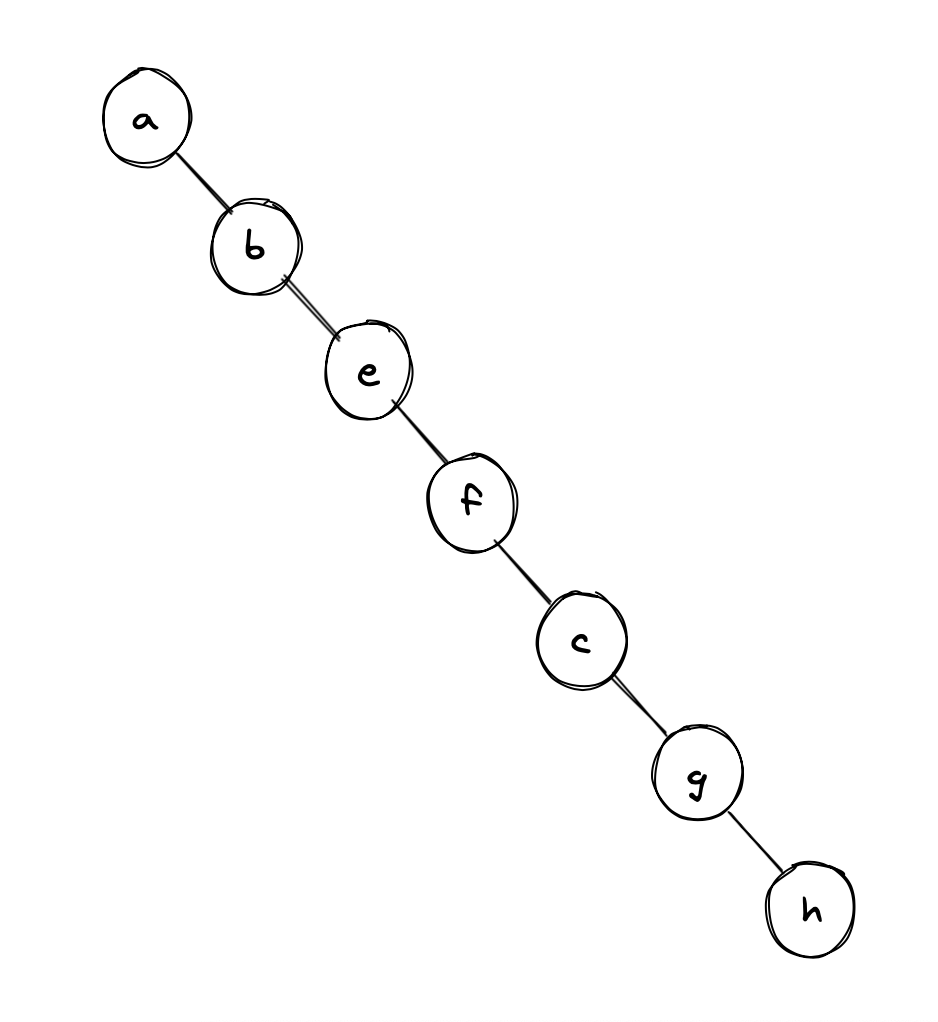
Example 1:
Input:
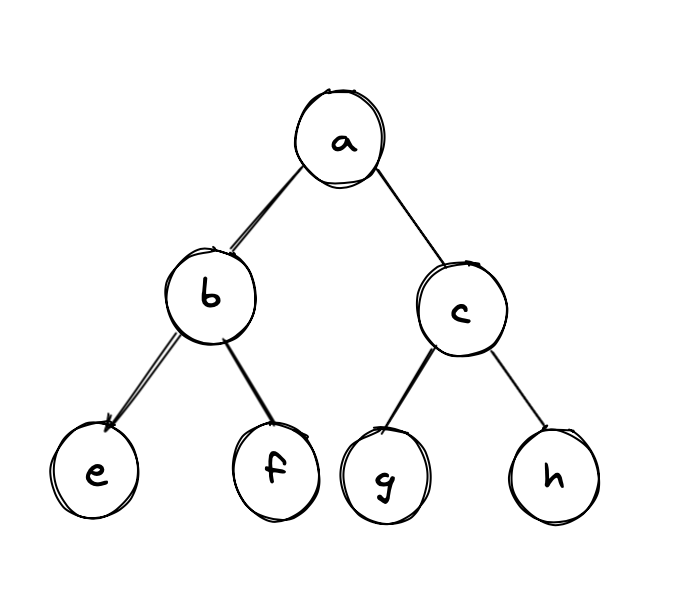
Output:
Example 2:
Input:
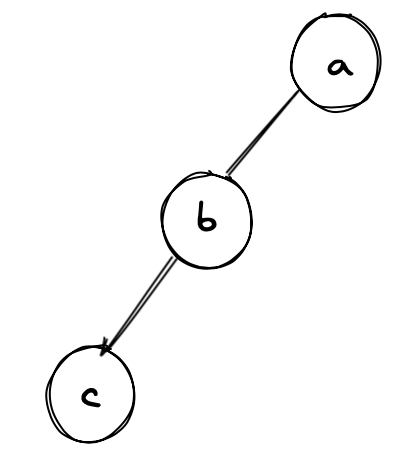
Output:
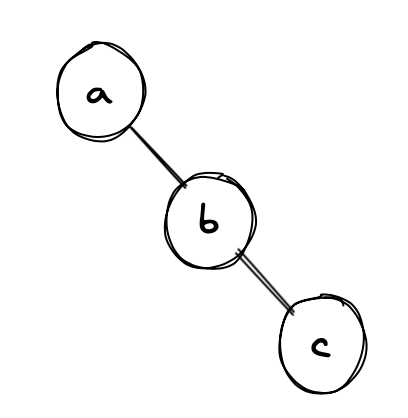
Example 3:
Input:
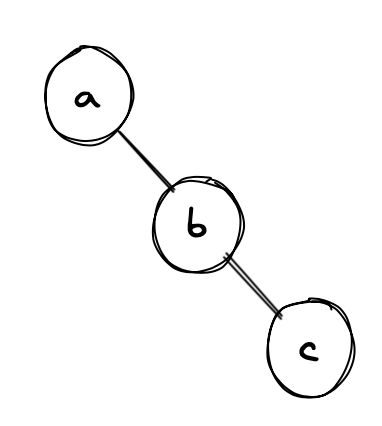
Output:
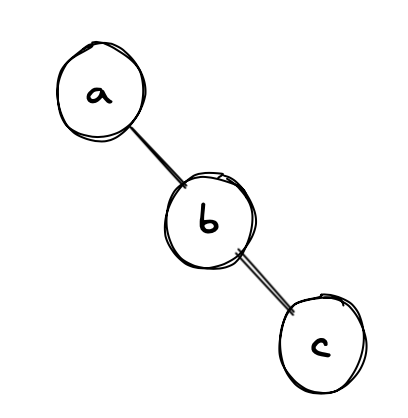
Match
Lists
// traverse tree:
preorder.append(nodes)
// traverse preorder:
build linked list
- we could implement this algorithm using list
- however this might not be the ideal solution since the linked list should use the same TreeNode class.
- complexity
- time: O(n) + O(n) ≈ O(n)
- space: O(n) + O(n) ≈ O(n)
Techniques
To solve a problem related to binary tree, it is a good idea to explore the techniques as well
- two ways we could traverse a binary tree are BFS and DFS
- since the linked list must be same as a pre-order traversal of the binary tree we need to traverse the tree in a pre-order traversal
Plan
- we will have to process nodes in a pre-order fashion and rewire the tree such that each node’s left is pointing to null and right pointer points to the left child of the node
- in order to traverse a tree DFS way, we have to traverse the entire branch of the tree and then the adjacent nodes
- in order to keep track of the node to be processed next it requires last in first out approach which can be tracked using a stack
- once the depth is reached the nodes are popped out of stack
- in oder to do so we will initialize a stack, with it’s first entry being the root of the given binary tree
- for every node,
- if a node has a left child, make it null
- make the node the new right child of the previous node
// initialize temp = tree node
// traverse tree iteratively
node = root
temp.left_chid = None
temp.right_child = node
temp = temp.right_child
Implement
def flatten(root: TreeNode) -> None:
if root == None:
return None
temp = TreeNode()
node_stack = [root]
while node_stack :
node = node_stack.pop()
temp.left = None
temp.right = node
if node.right:
node_stack.append(node.right)
if node.left:
node_stack.append(node.left)
temp = temp.right
Review
Consider the following input
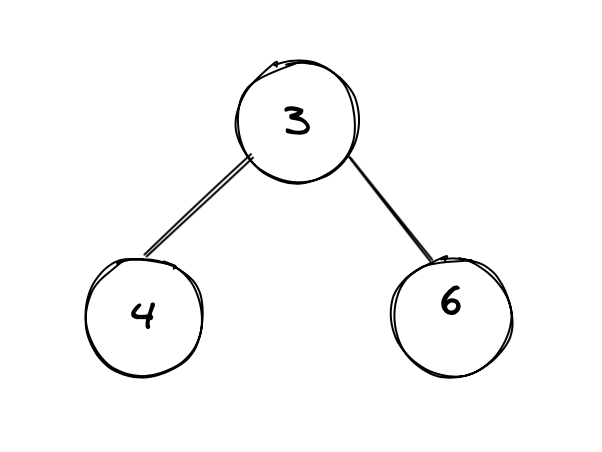
Output would be
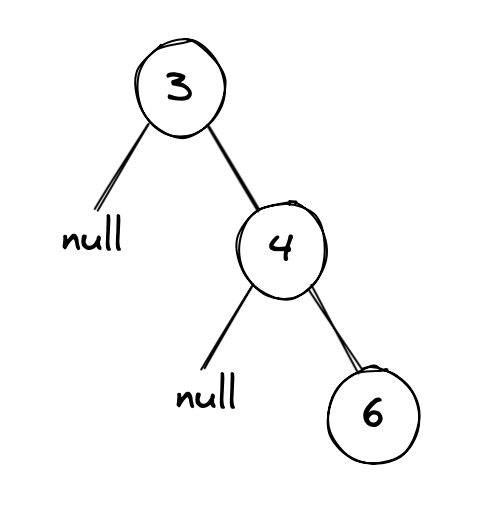
Evaluate
Complexity:
- time: O(n)
- space: O(n)