Validate subsequence

Solving this problem helped me understand the order of techniques I can explore to arrive at the solution for an array problem.

Problem statement

Given two non-empty arrays of integers, write a function that determines whether the second array is a subsequence of the first one.

A subsequence of an array is a set od numbers that aren’t necessarily adjacent in the array but that are in the same order as they appear in the array.

Understand

Input:

• array = [1,2,3,4,5,6,7,8],
• subsequence = [3,5,7] Output: true

Input:

• array: [10,20,30,40,50]
• subsequence: [40] Output: true

Input:

• array = [11,11,11,11]
• subsequence: [12,13,14] Output: false

Input:

• array: [5,1,22,25,6,-1,8,10]
• subsequence: [1,6,-1,-2] Output: false

Input:

• array: []
• subsequence: [2,4,5] Output: Invalid case

Match and Plan

List

• iterate subsequence check for the numbers of subsequence are also present in input array and are in same order
• O(n^2) solution
• NOTE: with this plan, we cannot handle the duplicate numbers in the array of in the sequence

Linked List

• complicates the solution

Sets

• with sets we cannot:
  • handle the duplicate values
  • maintain the order of numbers

Dictionaries

• iterate through sequence
• build a hashmap,
  • if keys are numbers of the sequence and values are the index of the number in sequence
    • will fail in handling duplicate numbers
  • if keys are the index of the numbers in the sequence and values are the numbers themselves
    • we won’t be able to check if a number in array is present in dictionary in constant time

Techniques

• build an array of all the possible sequence of the input array
• check if the given subsequence is present in the array of all the possible sequence of the input array

Pointers with pointers we can compare two numbers in the array and condition their movement accordingly. Pointers can also optimize the solution by not taking extra space

• initialize two index pointers to 0
• let one index pointer point to the numbers in sequence and the other to the numbers in array
• if array[array_index] == sequence[sequence_index], increment sequence_index to check the next number in the sequence
• increment array_index regardless
• return true of all the numbers in the sequence are covered

Implement

def isValidSubsequence(array, sequence):
    arr_idx = 0
	seq_idx = 0
	
	while arr_idx < len(array) and seq_idx < len(sequence): 
		if sequence[seq_idx] == array[arr_idx]:
			seq_idx += 1
		arr_idx += 1
	
	return seq_idx == len(sequence)	

Review

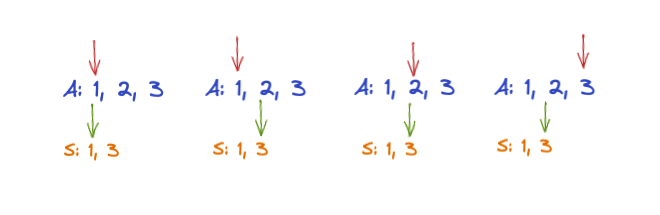
lets dry run the code with the following test case:
array = [1,2,3], sequence = [1,3]

Evaluate

Complexity:

• time: O(n), where n = len(array)
• space: O(1)