Walls and gates - Breadth first search

Problem statement
Given a m x n grid rooms initialized with these three possible values.
- -1 A wall or an obstacle.
- 0 A gate.
- INF Infinity means an empty room. We use the value 2 31 - 1 = 2147483647 to represent INF as you may assume that the distance to a gate is less than 2147483647.
Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.
Understand
Example 1:
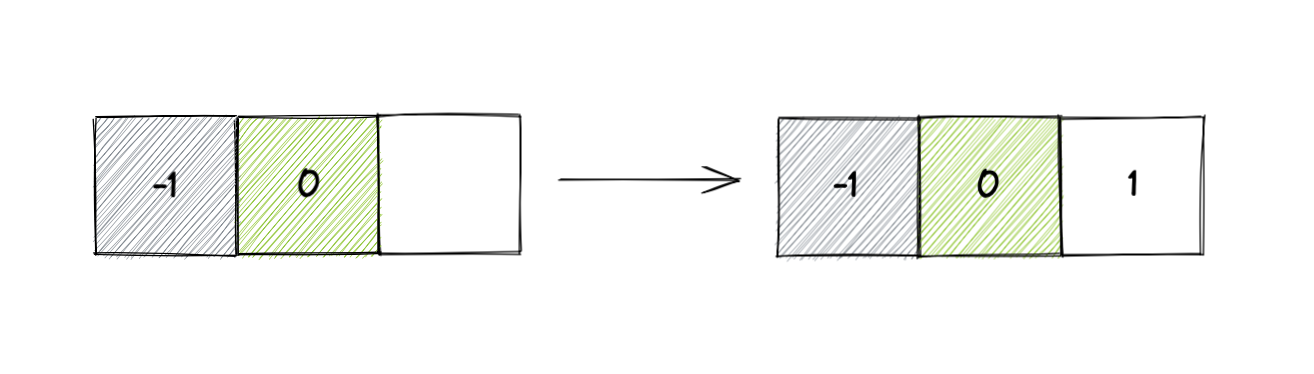
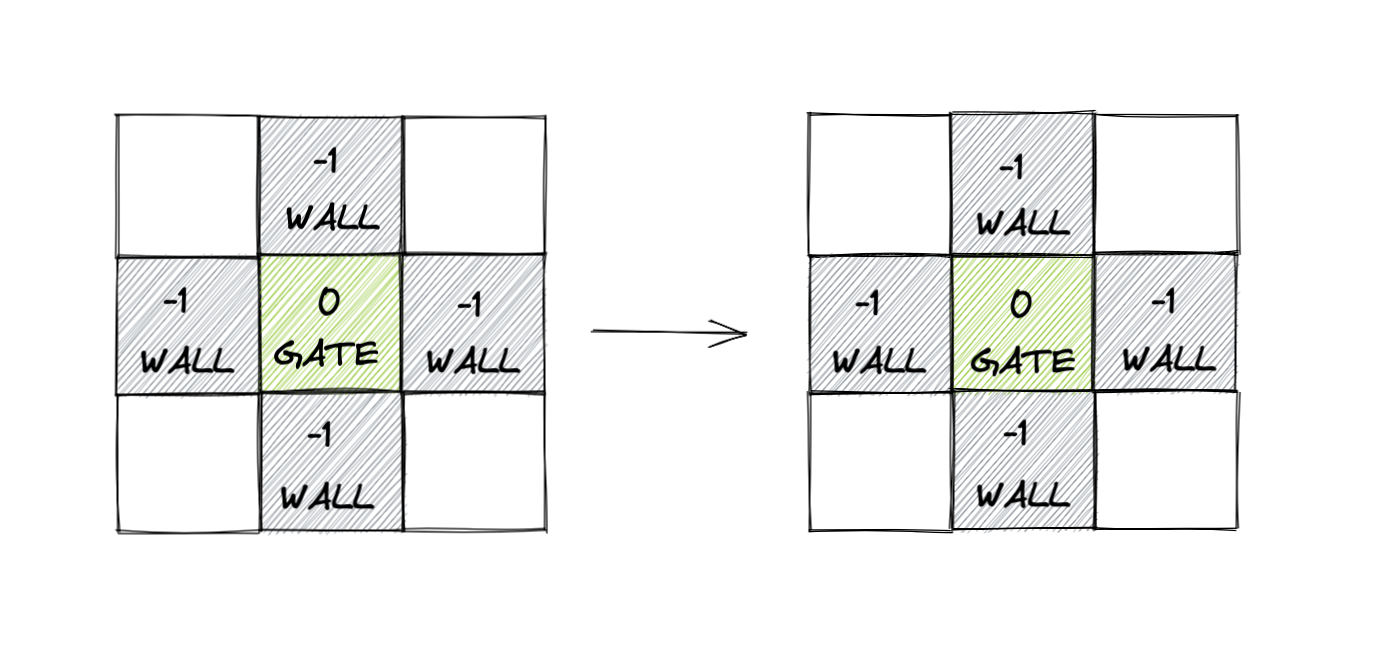
Example 2:
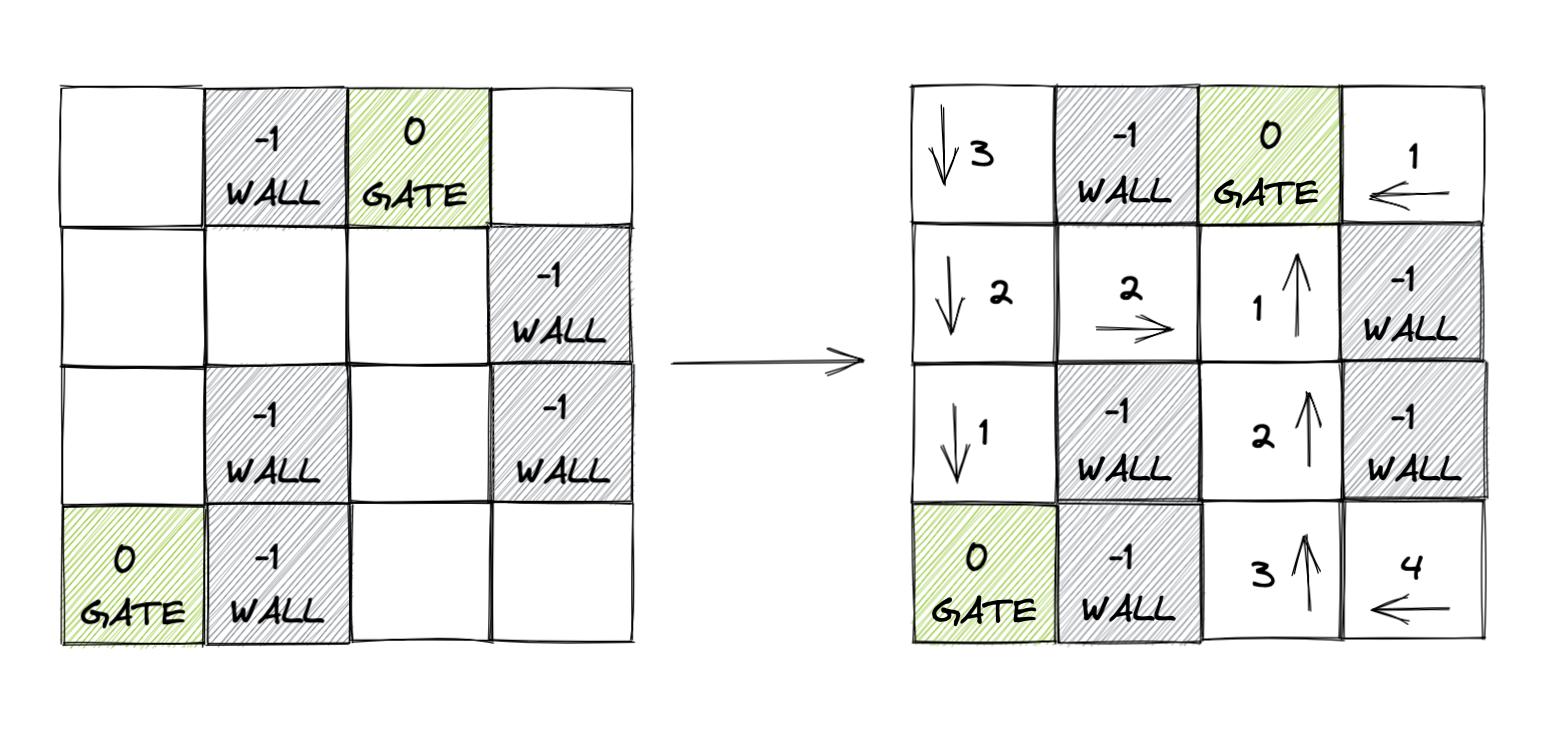
Example 3:
Match and plan
- From the gate we have to go to the neighboring cells and mark the cells with the shortest distance from the nearest gate
- This is graph problem where we have to traverse the given matrix and update the values in the cells
- We can traverse the matrix with BFS or DFS way
- I have used BFS to traverse the matrix because we have to find the shortest distance and BFS will help us find the shortest distance
Logical steps:
- from main function call BFS function
- source cell is the fist cell with value = 0 (gate)
- go to neighbors of the source and change the value of the neighboring cell with minimum(value of cell, distance)
- perform above step only if
- value != -1 (wall)
- value != 0 (gate)
- if cell is not visited
So the first wo conditions where we are avoiding visiting a cell is the additional conditions we must take care in solving this problem
Implement
def valid_neighbors(r,c,row,col):
valid = []
neighbors = [(r,c-1),(r,c+1),(r-1,c),(r+1,c)]
for (nr,nc) in neighbors:
if row > nr >= 0 and col > nc >= 0:
valid.append((nr,nc))
return valid
def bfs(ro, col, rooms):
visited = set()
queue = [(ro, col)]
visited.add((ro,col))
distance = 0
while queue:
for _ in range(len(queue)):
ro, col = queue.pop(0)
rooms[ro][col] = min(rooms[ro][col], distance)
for (nr,nc) in valid_neighbors(ro, col, len(rooms), len(rooms[0])):
if (nr,nc) not in visited and rooms[nr][nc] != -1 and rooms[nr][nc] != 0:
queue.append((nr,nc))
visited.add((nr,nc))
distance +=1
def wallsAndGates(rooms):
for row in range(len(rooms)):
for column in range(len(rooms[0])):
if rooms[row][column] == 0:
bfs(row, column, rooms)
- After discussing the above implementation with a few of my friends, I found their suggestions regarding implementing the code to get the valid neighbors of a cell helpful and adopted the following, which much easier to understand and read.
def valid_neighbors(r,c,row,col):
valid = []
neighbors = [(r,c-1),(r,c+1),(r-1,c),(r+1,c)]
for (nr,nc) in neighbors:
if 0 <= nr < row and 0 <= nc < col:
valid.append((nr,nc))
return valid
notice something about the “if condition”?
Alternatively
one might think of implementing the following logic to update the distance in the cell
for (nr,nc) in valid_neighbors(ro, col, len(rooms), len(rooms[0])):
if rooms[nr][nc] > distance:
rooms[nr][nc] = distance+1
queue.append((nr,nc,distance+1))
- in the above scenario we are not checking if the cells are already visited, instead checking if the values is the cell is greater than distance which works fine but it takes a longer computational time for a much bigger matrix as we are have to visit all the cells
- in order to avoid this we could update the cell with min(rooms[ro][col], distance) and amend our code as follows
rooms[ro][col] = min(rooms[ro][col], distance)
for (nr,nc) in valid_neighbors(ro, col, len(rooms), len(rooms[0])):
if (nr,nc) not in visited and rooms[nr][nc] != -1 and rooms[nr][nc] != 0:
queue.append((nr,nc))
visited.add((nr,nc))
distance +=1
Evaluate
Complexity
- time: O(omg), where o = number of rows, m = number of columns and g = number of gates
- BFS takes m*n steps to reach a all rooms a gate
- BFS from every single gate
- space: O(om), where o is number of rows and m is number of columns
- we are making use of a queue in BFS to explore the unvisited cells
- visited set
Leaving with a question: How can we optimize time complexity and make it O(om). I shall explore this in my next post