The following problem helped me understand that in-order traversal of a binary search tree yields a sorted array.

Problem statement

Write a function that takes in a Binary Search Tree(BST) and a positive integer k and returns the kth largest integer contained in the BST

Assume the following:

there will only be integer values in the BST
k <= number of nodes in the BST
if tree = [5, 7, 7] second largest value of the BST will be 7 and not 5

Understand

Input: [15, 5, 20, 2, 5, 17, 22, 1, 3],k = 3
Output: 17

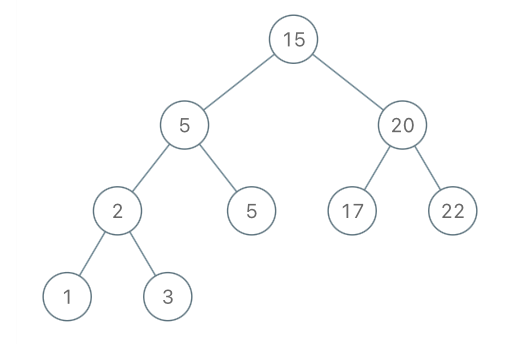
Explanation: after 22 and 20, 17 is the largest values in the given BST

Input: [1], k=1
Output: 1

Input: [1], k=2
Output: not a valid case

Input: [2,1,3], k=3
Output: 3

Input: [1,null,2,null,3,null,4], k=0
Output: Not a valid case

Match

List

// traverse tree 
    build node_list 
// sort nodes_list in descending order
// return node_list[k]

complexity:
- time: O(n)+O(n log n) -> O(n log n)
- space: O(n)

Linked list

using linked list will cost us extra time to create a liked list

Hashmap asd Hashset

both the data structure are not useful for solving the problem

Stack and Queue

we are not required to look for or maintain LIFO or FIFO order

Heap

Heap are very helpful to find the kth largest or kth smallest elements
```
// create max heap
// pop k times 
// return kth popped item 
```
complexity:
- time: O(n) + O(n log n) -> O(n log n)
- space: O(n)
all though with heap we can obtain the kth element, it did not improve the complexity of the algorithm that we came up by using list

Techniques

we can traverse a tree using BFS or DFS
DFS has preorder, postorder and inorder traversal

Exploring the traversals

let us consider out first example, tree = [15,5,20,2,5,17,22,1,3] and check the order of the nodes that we visit with each traversal

Breadth first search

bfs traversal of BST = [[1],[2,3],[5,5,15,17],[20,22]]

Preorder traversal

preorder traversal of BST = [15,5,20,2,5,17,22,1,3] is [15,5,2,1,3,5,20,17,22]

Postorder traversal

postorder traversal of BST = [15,5,20,2,5,17,22,1,3] is [1,3,2,5,5,17,22,20,15]

Inorder traversal

inorder traversal of BST = [15,5,20,2,5,17,22,1,3] is [1,2,3,5,5,15,17,20,22]
comparing all the traversals it is safe to conclude that in-order traversal yields a sorted array
taking advantage of this property we can arrive at the solution arrive at the solution
high level steps involved are
- traverse tree in inorder fashion - build array of nodes
- return array[len(array)-k]

// dfs - inorder recursive 
// list of nodes
// return kth element from end

complexity:
- time: O(n)
- space: O(n)+O(n) -> O(n)
we could traverse the tree in reverse in-order to get the list of values in descending order
we can do so by adding left child on to the stack an then the right child so the right child is processed before the left child

// reverse in-order -> recursion
// list of nodes 
// return kth element 

complexity:
- time: O(n)
- space: O(n)+O(n)

Implementation

class BST:
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

def reverse_inorder(root, array, k):
	if root == None:
		return None
	node = root
	stack = [node]
	while stack:
		if node == None:
			node = stack.pop() 
			array.append(node.value) 
			node = node.left
		else:
			stack.append(node)
			node = node.right
	
def findKthLargestValueInBst(tree, k):
	if tree == None:
		return None
	nodes_list = []
	reverse_inorder(tree, nodes_list, k)
    return nodes_list[k-1]

Review

for the input tree [15, 5, 20, 2, 5, 17, 22, 1, 3] and k = 3
- nodes_list = [22, 20, 17, 15, 5, 5, 3, 2, 1, 15]

Evaluate:

complexity:
- traverse tree -> time: O(n)
- nodes_list + call stack -> space: O(n)+O(n)